Quantum Information And Computation

• Paper 4, Section I, 10D

  Quantum Information and Computation

  Part II, 2018

  Let $B_{n}$ denote the set of all $n$-bit strings. Suppose we are given a 2-qubit quantum gate $I_{x_{0}}$ which is promised to be of the form

  $$I_{x_{0}}|x\rangle=\left\{\begin{array}{rr} |x\rangle & x \neq x_{0} \\ -|x\rangle & x=x_{0} \end{array}\right.$$

  but the 2-bit string $x_{0}$ is unknown to us. We wish to determine $x_{0}$ with the least number of queries to $I_{x_{0}}$. Define $A=I-2|\psi\rangle\langle\psi|$, where $I$ is the identity operator and $|\psi\rangle=\frac{1}{2} \sum_{x \in B_{2}}|x\rangle$.

  (a) Is $A$ unitary? Justify your answer.

  (b) Compute the action of $I_{x_{0}}$ on $|\psi\rangle$, and the action of $|\psi\rangle\langle\psi|$ on $\left|x_{0}\right\rangle$, in each case expressing your answer in terms of $|\psi\rangle$ and $\left|x_{0}\right\rangle$. Hence or otherwise show that $x_{0}$ may be determined with certainty using only one application of the gate $I_{x_{0}}$, together with any other gates that are independent of $x_{0}$.

  (c) Let $f_{x_{0}}: B_{2} \rightarrow B_{1}$ be the function having value 0 for all $x \neq x_{0}$ and having value 1 for $x=x_{0}$. It is known that a single use of $I_{x_{0}}$ can be implemented with a single query to a quantum oracle for the function $f_{x_{0}}$. But suppose instead that we have a classical oracle for $f_{x_{0}}$, i.e. a black box which, on input $x$, outputs the value of $f_{x_{0}}(x)$. Can we determine $x_{0}$ with certainty using a single query to the classical oracle? Justify your answer.

  comment

• Paper 3, Section I, 10D

  Quantum Information and Computation

  Part II, 2018

  Let $B_{n}$ denote the set of all $n$-bit strings. For any Boolean function on 2 bits $f: B_{2} \rightarrow B_{1}$ consider the linear operation on 3 qubits defined by

  $$U_{f}|x\rangle|y\rangle=|x\rangle|y \oplus f(x)\rangle$$

  for all $x \in B_{2}, y \in B_{1}$ and $\oplus$ denoting addition of bits modulo 2 . Here the first register is a 2-qubit register and the second is a 1-qubit register. We are able to apply only the 1-qubit Pauli $X$ and Hadamard $H$ gates to any desired qubits, as well as the 3 -qubit gate $U_{f}$ to any three qubits. We can also perform measurements in the computational basis.

  (a) Describe how we can construct the state

  $$|f\rangle=\frac{1}{2} \sum_{x \in B_{2}}(-1)^{f(x)}|x\rangle$$

  starting from the standard 3-qubit state $|0\rangle|0\rangle|0\rangle$.

  (b) Suppose now that the gate $U_{f}$ is given to us but $f$ is not specified. However $f$ is promised to be one of two following cases:

  (i) $f$ is a constant function (i.e. $f(x)=0$ for all $x$, or $f(x)=1$ for all $x$ ),

  (ii) for any 2-bit string $x=b_{1} b_{2}$ we have $f\left(b_{1} b_{2}\right)=b_{1} \oplus b_{2}$ (with $\oplus$ as above).

  Show how we may determine with certainty which of the two cases (i) or (ii) applies, using only a single application of $U_{f}$.

  comment

• Paper 2, Section I, $10 D$

  Quantum Information and Computation

  Part II, 2018

  (a) The classical controlled- $N O T$ operation applied to the 2-bit string $b 0$ (for $b=0$ or 1 ) achieves the cloning of $b$, i.e. the result is $b b$. Let $C X$ denote the quantum controlled$X$ (or controlled-NOT) operation on two qubits. For which qubit states $|\psi\rangle=a|0\rangle+b|1\rangle$ will the application of $C X$ to $|\psi\rangle|0\rangle$ (with the first qubit being the control qubit) achieve the cloning of $|\psi\rangle$ ? Justify your answer.

  (b) Let $\left|\alpha_{0}\right\rangle$ and $\left|\alpha_{1}\right\rangle$ be two distinct non-orthogonal quantum states. State and prove the quantum no-cloning theorem for unitary processes.

  comment

• Paper 1, Section I, D

  Quantum Information and Computation

  Part II, 2018

  (a) Define what it means for a 2-qubit state $|\psi\rangle_{A B}$ of a composite quantum system $A B$ to be entangled.

  Consider the 2-qubit state

  $$|\alpha\rangle=\frac{1}{\sqrt{3}}(2|00\rangle-H \otimes H|11\rangle)$$

  where $H$ is the Hadamard gate. From the definition of entanglement, show that $|\alpha\rangle$ is an entangled state.

  (b) Alice and Bob are distantly separated in space. Initially they each hold one qubit of the 2-qubit entangled state

  $$\left|\phi^{+}\right\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)$$

  They are able to perform local quantum operations (unitary gates and measurements) on quantum systems they hold. Alice wants to communicate two classical bits of information to Bob. Explain how she can achieve this (within their restricted operational resources) by sending him a single qubit.

  comment

• Paper 2, Section II, D

  Quantum Information and Computation

  Part II, 2018

  (a) Suppose that Alice and Bob are distantly separated in space and each has one qubit of the 2-qubit state $\left|\phi^{+}\right\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)$. They also have the ability to perform local unitary quantum operations and local computational basis measurements, and to communicate only classically. Alice has a 1-qubit state $|\alpha\rangle$ (whose identity is unknown to her) which she wants to communicate to Bob. Show how this can be achieved using only the operational resources, listed above, that they have available.

  Suppose now that a third party, called Charlie, joins Alice and Bob. They are all mutually distantly separated in space and each holds one qubit of the 3-qubit state

  $$|\gamma\rangle=\frac{1}{\sqrt{2}}(|000\rangle+|111\rangle) .$$

  As previously with Alice and Bob, they are able to communicate with each other only classically, e.g. by telephone, and they can each also perform only local unitary operations and local computational basis measurements. Alice and Bob phone Charlie to say that they want to do some quantum teleportation and they need a shared $\left|\phi^{+}\right\rangle$state (as defined above). Show how Charlie can grant them their wish (with certainty), given their joint possession of $|\gamma\rangle$ and using only their allowed operational resources. [Hint: It may be useful to consider application of an appropriate Hadamard gate action.]

  (b) State the quantum no-signalling principle for a bipartite state $|\psi\rangle_{A B}$ of the composite system $A B$.

  Suppose we are given an unknown one of the two states

  $$\begin{aligned} &\left|\phi^{+}\right\rangle_{A B}=\frac{1}{\sqrt{2}}\left(|00\rangle_{A B}+|11\rangle_{A B}\right) \\ &\left|\phi^{-}\right\rangle_{A B}=\frac{1}{\sqrt{2}}\left(|00\rangle_{A B}-|11\rangle_{A B}\right) \end{aligned}$$

  and we wish to identify which state we have. Show that the minimum error probability for this state discrimination task is zero.

  Suppose now that we have access only to qubit $B$ of the received state. Show that we can now do no better in the state discrimination task than just making a random guess as to which state we have.

  comment

• Paper 3, Section II, $15 \mathrm{D}$

  Quantum Information and Computation

  Part II, 2018

  In this question you may assume the following fact about the quantum Fourier transform $Q F T \bmod N:$ if $N=A r$ and $0 \leqslant x_{0}<r$, where $A, r, x_{0} \in \mathbb{Z}$, then

  $$Q F T \frac{1}{\sqrt{A}} \sum_{k=0}^{A-1}\left|x_{0}+k r\right\rangle=\frac{1}{\sqrt{r}} \sum_{l=0}^{r-1} \omega^{x_{0} l A}|l A\rangle$$

  where $\omega=e^{2 \pi i / N}$.

  (a) Let $\mathbb{Z}_{N}$ denote the integers modulo $N$. Let $f: \mathbb{Z}_{N} \rightarrow \mathbb{Z}$ be a periodic function with period $r$ and with the property that $f$ is one-to-one within each period. We have one instance of the quantum state

  $$|f\rangle=\frac{1}{\sqrt{N}} \sum_{x=0}^{N-1}|x\rangle|f(x)\rangle$$

  and the ability to calculate the function $f$ on at most two $x$ values of our choice.

  Describe a procedure that may be used to determine the period $r$ with success probability $O(1 / \log \log N)$. As a further requirement, at the end of the procedure we should know if it has been successful, or not, in outputting the correct period value. [You may assume that the number of integers less than $N$ that are coprime to $N$ is $O(N / \log \log N)]$.

  (b) Consider the function $f: \mathbb{Z}_{12} \rightarrow \mathbb{Z}_{10}$ defined by $f(x)=3^{x} \bmod 10$.

  (i) Show that $f$ is periodic and find the period.

  (ii) Suppose we are given the state $|f\rangle=\frac{1}{\sqrt{12}} \sum_{x=0}^{11}|x\rangle|f(x)\rangle$ and we measure the second register. What are the possible resulting measurement values $y$ and their probabilities?

  (iii) Suppose the measurement result was $y=3$. Find the resulting state $|\alpha\rangle$ of the first register after the measurement.

  (iv) Suppose we measure the state $Q F T|\alpha\rangle$ (with $|\alpha\rangle$ from part (iii)). What is the probability of each outcome $0 \leqslant c \leqslant 11$ ?

  comment

• Paper 4, Section I, $10 D$

  Quantum Information and Computation

  Part II, 2019

  (a) Define the order of $\alpha \bmod N$ for coprime integers $\alpha$ and $N$ with $\alpha<N$. Explain briefly how knowledge of this order can be used to provide a factor of $N$, stating conditions on $\alpha$ and its order that must be satisfied.

  (b) Shor's algorithm for factoring $N$ starts by choosing $\alpha<N$ coprime. Describe the subsequent steps of a single run of Shor's algorithm that computes the order of $\alpha$ mod $N$ with probability $O(1 / \log \log N)$.

  [Any significant theorems that you invoke to justify the algorithm should be clearly stated (but proofs are not required). In addition you may use without proof the following two technical results.

  Theorem $F T$ : For positive integers $t$ and $M$ with $M \geqslant t^{2}$, and any $0 \leqslant x_{0}<t$, let $K$ be the largest integer such that $x_{0}+(K-1) t<M .$ Let QFT denote the quantum Fourier transform $\bmod M$. Suppose we measure $Q F T\left(\frac{1}{\sqrt{K}} \sum_{k=0}^{K-1}\left|x_{0}+k t\right\rangle\right)$ to obtain an integer $c$ with $0 \leqslant c<M .$ Then with probability $O(1 / \log \log t), c$ will be an integer closest to a multiple $j(M / t)$ of $M / t$ for which the value of $j$ (between 0 and $t$ ) is coprime to $t$.

  Theorem CF: For any rational number $a / b$ with $0<a / b<1$ and with integers a and $b$ having at most $n$ digits each, let $p / q$ with $p$ and $q$ coprime, be any rational number satisfying

  $$\left|\frac{a}{b}-\frac{p}{q}\right| \leqslant \frac{1}{2 q^{2}} .$$

  Then $p / q$ is one of the $O(n)$ convergents of the continued fraction of $a / b$ and all the convergents can be classically computed from $a / b$ in time $O\left(n^{3}\right)$.]

  comment

• Paper 3, Section I, $10 D$

  Quantum Information and Computation

  Part II, 2019

  Let $B_{n}$ denote the set of all $n$-bit strings and write $N=2^{n}$. Let $I$ denote the identity operator on $n$ qubits and for $G=\left\{x_{1}, x_{2}, \ldots, x_{k}\right\} \subset B_{n}$ introduce the $n$-qubit operator

  $$Q=-H_{n} I_{0} H_{n} I_{G}$$

  where $H_{n}=H \otimes \ldots \otimes H$ is the Hadamard operation on each of the $n$ qubits, and $I_{0}$ and $I_{G}$ are given by

  $$I_{0}=I-2|00 \ldots 0\rangle\left\langle 00 \ldots 0\left|\quad I_{G}=I-2 \sum_{x \in G}\right| x\right\rangle\langle x|$$

  Also introduce the states

  $$\left|\psi_{0}\right\rangle=\frac{1}{\sqrt{N}} \sum_{x \in B_{n}}|x\rangle \quad\left|\psi_{G}\right\rangle=\frac{1}{\sqrt{k}} \sum_{x \in G}|x\rangle \quad\left|\psi_{B}\right\rangle=\frac{1}{\sqrt{N-k}} \sum_{x \notin G}|x\rangle$$

  Let $\mathcal{P}$ denote the real span of $\left|\psi_{0}\right\rangle$ and $\left|\psi_{G}\right\rangle$.

  (a) Show that $Q$ maps $\mathcal{P}$ to itself, and derive a geometrical interpretation of the action of $Q$ on $\mathcal{P}$, stating clearly any results from Euclidean geometry that you use.

  (b) Let $f: B_{n} \rightarrow B_{1}$ be the Boolean function such that $f(x)=1$ iff $x \in G$. Suppose that $k=N / 4$. Show that we can obtain an $x \in G$ with certainty by using just one application of the standard quantum oracle $U_{f}$ for $f$ (together with other operations that are independent of $f$ ).

  comment

• Paper 2, Section I, $10 D$

  Quantum Information and Computation

  Part II, 2019

  The BB84 quantum key distribution protocol begins with Alice choosing two uniformly random bit strings $X=x_{1} x_{2} \ldots x_{m}$ and $Y=y_{1} y_{2} \ldots y_{m}$.

  (a) In terms of these strings, describe Alice's process of conjugate coding for the BB84 protocol.

  (b) Suppose Alice and Bob are distantly separated in space and have available a noiseless quantum channel on which there is no eavesdropping. They can also communicate classically publicly. For this idealised situation, describe the steps of the BB84 protocol that results in Alice and Bob sharing a secret key of expected length $m / 2$.

  (c) Suppose now that an eavesdropper Eve taps into the channel and carries out the following action on each passing qubit. With probability $1-p$, Eve lets it pass undisturbed, and with probability $p$ she chooses a bit $w \in\{0,1\}$ uniformly at random and measures the qubit in basis $B_{w}$ where $B_{0}=\{|0\rangle,|1\rangle\}$ and $B_{1}=\{(|0\rangle+|1\rangle) / \sqrt{2},(|0\rangle-|1\rangle) / \sqrt{2}\}$. After measurement Eve sends the post-measurement state on to Bob. Calculate the bit error rate for Alice and Bob's final key in part (b) that results from Eve's action.

  comment

• Paper 1, Section I, $10 D$ Introduce the 2 -qubit states

  Quantum Information and Computation

  Part II, 2019

  $$\left|\beta_{x z}\right\rangle=\left(Z^{z} X^{x}\right) \otimes I\left(\frac{|00\rangle+|11\rangle}{\sqrt{2}}\right)$$

  where $X$ and $Z$ are the standard qubit Pauli operations and $x, z \in\{0,1\}$.

  (a) For any 1-qubit state $|\alpha\rangle$ show that the 3 -qubit state $|\alpha\rangle_{C}\left|\beta_{00}\right\rangle_{A B}$ of system $C A B$ can be expressed as

  $$|\alpha\rangle_{C}\left|\beta_{00}\right\rangle_{A B}=\frac{1}{2} \sum_{x, z=0}^{1}\left|\beta_{x z}\right\rangle_{C A}\left|\mu_{x z}\right\rangle_{B}$$

  where the 1 -qubit states $\left|\mu_{x z}\right\rangle$ are uniquely determined. Show that $\left|\mu_{10}\right\rangle=X|\alpha\rangle$.

  (b) In addition to $\left|\mu_{10}\right\rangle=X|\alpha\rangle$ you may now assume that $\left|\mu_{x z}\right\rangle=X^{x} Z^{z}|\alpha\rangle$. Alice and Bob are separated distantly in space and share a $\left|\beta_{00}\right\rangle_{A B}$ state with $A$ and $B$ labelling qubits held by Alice and Bob respectively. Alice also has a qubit $C$ in state $|\alpha\rangle$ whose identity is unknown to her. Using the results of part (a) show how she can transfer the state of $C$ to Bob using only local operations and classical communication, i.e. the sending of quantum states across space is not allowed.

  (c) Suppose that in part (b), while sharing the $\left|\beta_{00}\right\rangle_{A B}$ state, Alice and Bob are also unable to engage in any classical communication, i.e. they are able only to perform local operations. Can Alice now, perhaps by a modified process, transfer the state of $C$ to Bob? Give a reason for your answer.

  comment

• Paper 3, Section II, D

  Quantum Information and Computation

  Part II, 2019

  Let $\mathcal{H}_{d}$ denote a $d$-dimensional state space with orthonormal basis $\left\{|y\rangle: y \in \mathbb{Z}_{d}\right\}$. For any $f: \mathbb{Z}_{m} \rightarrow \mathbb{Z}_{n}$ let $U_{f}$ be the operator on $\mathcal{H}_{m} \otimes \mathcal{H}_{n}$ defined by

  $$U_{f}|x\rangle|y\rangle=|x\rangle|y+f(x) \bmod n\rangle$$

  for all $x \in \mathbb{Z}_{m}$ and $y \in \mathbb{Z}_{n}$.

  (a) Define $Q F T$, the quantum Fourier transform $\bmod d$ (for any chosen $d)$.

  (b) Let $S$ on $\mathcal{H}_{d}$ (for any chosen $d$ ) denote the operator defined by

  $$S|y\rangle=|y+1 \bmod d\rangle$$

  for $y \in \mathbb{Z}_{d}$. Show that the Fourier basis states $\left|\xi_{x}\right\rangle=Q F T|x\rangle$ for $x \in \mathbb{Z}_{d}$ are eigenstates of $S$. By expressing $U_{f}$ in terms of $S$ find a basis of eigenstates of $U_{f}$ and determine the corresponding eigenvalues.

  (c) Consider the following oracle promise problem:

  Input: an oracle for a function $f: \mathbb{Z}_{3} \rightarrow \mathbb{Z}_{3}$.

  Promise: $f$ has the form $f(x)=s x+t$ where $s$ and $t$ are unknown coefficients (and with all arithmetic being $\bmod 3)$.

  Problem: Determine $s$ with certainty.

  Can this problem be solved by a single query to a classical oracle for $f$ (and possible further processing independent of $f)$ ? Give a reason for your answer.

  Using the results of part (b) or otherwise, give a quantum algorithm for this problem that makes just one query to the quantum oracle $U_{f}$ for $f$.

  (d) For any $f: \mathbb{Z}_{3} \rightarrow \mathbb{Z}_{3}$, let $f_{1}(x)=f(x+1)$ and $f_{2}(x)=-f(x)$ (all arithmetic being $\bmod 3$ ). Show how $U_{f_{1}}$ and $U_{f_{2}}$ can each be implemented with one use of $U_{f}$ together with other unitary gates that are independent of $f$.

  (e) Consider now the oracle problem of the form in part (c) except that now $f$ is a quadratic function $f(x)=a x^{2}+b x+c$ with unknown coefficients $a, b, c$ (and all arithmetic being mod 3), and the problem is to determine the coefficient $a$ with certainty. Using the results of part (d) or otherwise, give a quantum algorithm for this problem that makes just two queries to the quantum oracle for $f$.

  comment

• Paper 2, Section II, D

  Quantum Information and Computation

  Part II, 2019

  Let $\left|\alpha_{0}\right\rangle \neq\left|\alpha_{1}\right\rangle$ be two quantum states and let $p_{0}$ and $p_{1}$ be associated probabilities with $p_{0}+p_{1}=1, p_{0} \neq 0, p_{1} \neq 0$ and $p_{0} \geqslant p_{1}$. Alice chooses state $\left|\alpha_{i}\right\rangle$ with probability $p_{i}$ and sends it to Bob. Upon receiving it, Bob performs a 2-outcome measurement $\mathcal{M}$ with outcomes labelled 0 and 1 , in an attempt to identify which state Alice sent.

  (a) By using the extremal property of eigenvalues, or otherwise, show that the operator $D=p_{0}\left|\alpha_{0}\right\rangle\left\langle\alpha_{0}\left|-p_{1}\right| \alpha_{1}\right\rangle\left\langle\alpha_{1}\right|$ has exactly two nonzero eigenvalues, one of which is positive and the other negative.

  (b) Let $P_{S}$ denote the probability that Bob correctly identifies Alice's sent state. If the measurement $\mathcal{M}$ comprises orthogonal projectors $\left\{\Pi_{0}, \Pi_{1}\right\}$ (corresponding to outcomes 0 and 1 respectively) give an expression for $P_{S}$ in terms of $p_{1}, \Pi_{0}$ and $D$.

  (c) Show that the optimal success probability $P_{S}^{\text {opt }}$, i.e. the maximum attainable value of $P_{S}$, is

  $$P_{S}^{\mathrm{opt}}=\frac{1+\sqrt{1-4 p_{0} p_{1} \cos ^{2} \theta}}{2}$$

  where $\cos \theta=\left|\left\langle\alpha_{0} \mid \alpha_{1}\right\rangle\right|$.

  (d) Suppose we now place the following extra requirement on Bob's discrimination process: whenever Bob obtains output 0 then the state sent by Alice was definitely $\left|\alpha_{0}\right\rangle$. Show that Bob's $P_{S}^{\mathrm{opt}}$ now satisfies $P_{S}^{\mathrm{opt}} \geqslant 1-p_{0} \cos ^{2} \theta$.

  comment

• Paper 1, Section I, 10C

  Quantum Information and Computation

  Part II, 2020

  Suppose we measure an observable $A=\hat{n} \cdot \vec{\sigma}$on a qubit, where $\hat{n}=\left(n_{x}, n_{y}, n_{z}\right) \in \mathbb{R}^{3}$ is a unit vector and $\vec{\sigma}=\left(\sigma_{x}, \sigma_{y}, \sigma_{z}\right)$ is the vector of Pauli operators.

  (i) Express $A$ as a $2 \times 2$ matrix in terms of the components of $\hat{n}$.

  (ii) Representing $\hat{n}$ in terms of spherical polar coordinates as $\hat{n}=(1, \theta, \phi)$, rewrite the above matrix in terms of the angles $\theta$ and $\phi$.

  (iii) What are the possible outcomes of the above measurement?

  (iv) Suppose the qubit is initially in a state $|1\rangle$. What is the probability of getting an outcome 1?

  (v) Consider the three-qubit state

  $$|\psi\rangle=a|000\rangle+b|010\rangle+c|110\rangle+d|111\rangle+e|100\rangle$$

  Suppose the second qubit is measured relative to the computational basis. What is the probability of getting an outcome 1? State the rule that you are using.

  comment

• Paper 2, Section I, 10C

  Quantum Information and Computation

  Part II, 2020

  Consider the set of states

  $$\left|\beta_{z x}\right\rangle:=\frac{1}{\sqrt{2}}\left[|0 x\rangle+(-1)^{z}|1 \bar{x}\rangle\right],$$

  where $x, z \in\{0,1\}$ and $\bar{x}=x \oplus 1$ (addition modulo 2 ).

  (i) Show that

  $$(H \otimes \mathbb{I}) \circ \mathrm{CX}\left|\beta_{z x}\right\rangle=|z x\rangle \quad \forall z, x \in\{0,1\},$$

  where $H$ denotes the Hadamard gate and CX denotes the controlled- $X$ gate.

  (ii) Show that for any $z, x \in\{0,1\}$,

  $$\left(Z^{z} X^{x} \otimes \mathbb{I}\right)\left|\beta_{00}\right\rangle=\left|\beta_{z x}\right\rangle .$$

  [Hint: For any unitary operator $U$, we have $(U \otimes \mathbb{I})\left|\beta_{00}\right\rangle=\left(\mathbb{I} \otimes U^{T}\right)\left|\beta_{00}\right\rangle$, where $U^{T}$ denotes the transpose of $U$ with respect to the computational basis.]

  (iii) Suppose Alice and Bob initially share the state $\left|\beta_{00}\right\rangle$. Show using (*) how Alice can communicate two classical bits to Bob by sending him only a single qubit.

  comment

• Paper 3, Section I, $10 C$

  Quantum Information and Computation

  Part II, 2020

  For $\phi \in[0,2 \pi)$ and $|\psi\rangle \in \mathbb{C}^{4}$ consider the operator

  $$R_{\psi}^{\phi}=\mathbb{I}-\left(1-e^{i \phi}\right)|\psi\rangle\langle\psi|$$

  Let $U$ be a unitary operator on $\mathbb{C}^{4}=\mathbb{C}^{2} \otimes \mathbb{C}^{2}$ with action on $|00\rangle$ given as follows

  $$U|00\rangle=\sqrt{p}|g\rangle+\sqrt{1-p}|b\rangle=:\left|\psi_{\mathrm{in}}\right\rangle$$

  where $p$ is a constant in $[0,1]$ and $|g\rangle,|b\rangle \in \mathbb{C}^{4}$ are orthonormal states.

  (i) Give an explicit expression of the state $R_{g}^{\phi} U|00\rangle$.

  (ii) Find a $|\psi\rangle \in \mathbb{C}^{4}$ for which $R_{\psi}^{\pi}=U R_{00}^{\pi} U^{\dagger}$.

  (iii) Choosing $p=1 / 4$ in equation ( $\dagger$, calculate the state $U R_{00}^{\pi} U^{\dagger} R_{g}^{\phi} U|00\rangle$. For what choice of $\phi \in[0,2 \pi)$ is this state proportional to $|g\rangle$ ?

  (iv) Describe how the above considerations can be used to find a marked element $g$ in a list of four items $\left\{g, b_{1}, b_{2}, b_{3}\right\}$. Assume that you have the state $|00\rangle$ and can act on it with a unitary operator that prepares the uniform superposition of four orthonormal basis states $|g\rangle,\left|b_{1}\right\rangle,\left|b_{2}\right\rangle,\left|b_{3}\right\rangle$ of $\mathbb{C}^{4}$. [You may use the operators $U$ (defined in (†)), $U^{\dagger}$ and $R_{\psi}^{\phi}$ for any choice of $\phi \in[0,2 \pi)$ and any $|\psi\rangle \in \mathbb{C}^{4}$.]

  comment

• Paper 4, Section I, C

  Quantum Information and Computation

  Part II, 2020

  (i) What is the action of $\mathrm{QFT}_{N}$ on a state $|x\rangle$, where $x \in\{0,1,2, \ldots, N-1\}$ and $\mathrm{QFT}_{N}$ denotes the Quantum Fourier Transform modulo $N$ ?

  (ii) For the case $N=4$ write $0,1,2,3$ respectively in binary as $00,01,10,11$ thereby identifying the four-dimensional space as that of two qubits. Show that $\mathrm{QFT}_{N}|10\rangle$ is an unentangled state of the two qubits.

  (iii) Prove that $\left(\mathrm{QFT}_{N}\right)^{2}|x\rangle=|N-x\rangle$, where $\left(\mathrm{QFT}_{N}\right)^{2} \equiv \mathrm{QFT}_{N} \circ \mathrm{QFT}_{N}$.

  [Hint: For $\omega=e^{2 \pi i / N}, \sum_{m=0}^{N-1} \omega^{m K}=0$ if $K$ is not a multiple of $N$.]

  (iv) What is the action of $\left(\mathrm{QFT}_{N}\right)^{4}$ on a state $|x\rangle$, for any $x \in\{0,1,2, \ldots, N-1\}$ ? Use the above to determine what the eigenvalues of $\mathrm{QFT}_{N}$ are.

  comment

• Paper 2, Section II, 15C

  Quantum Information and Computation

  Part II, 2020

  (a) Show how the $n$-qubit state

  $$\left|\psi_{n}\right\rangle:=\frac{1}{\sqrt{2^{n}}} \sum_{x \in B_{n}}|x\rangle$$

  can be generated from a computational basis state of $\mathbb{C}^{n}$ by the action of Hadamard gates.

  (b) Prove that $C Z=(I \otimes H) C N O T_{12}(I \otimes H)$, where $C Z$ denotes the controlled- $Z$ gate. Justify (without any explicit calculations) the following identity:

  $$C N O T_{12}=(I \otimes H) C Z(I \otimes H)$$

  (c) Consider the following two-qubit circuit:

  

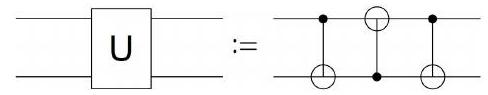
  What is its action on an arbitrary 2-qubit state $|\psi\rangle \otimes|\phi\rangle ?$ In particular, for two given states $|\psi\rangle$ and $|\phi\rangle$, find the states $|\alpha\rangle$ and $|\beta\rangle$ such that

  $$U(|\psi\rangle \otimes|\phi\rangle)=|\alpha\rangle \otimes|\beta\rangle .$$

  (d) Consider the following quantum circuit diagram

  

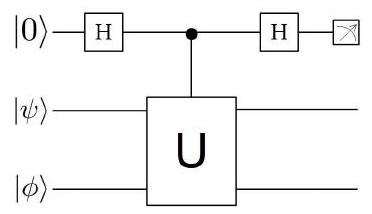
  where the measurement is relative to the computational basis and $U$ is the quantum gate from part (c). Note that the second gate in the circuit performs the following controlled operation:

  $$|0\rangle|\psi\rangle|\phi\rangle \mapsto|0\rangle|\psi\rangle|\phi\rangle ;|1\rangle|\psi\rangle|\phi\rangle \mapsto|1\rangle U(|\psi\rangle|\phi\rangle) .$$

  (i) Give expressions for the joint state of the three qubits after the action of the first Hadamard gate; after the action of the quantum gate $U$; and after the action of the second Hadamard gate.

  (ii) Compute the probabilities $p_{0}$ and $p_{1}$ of getting outcome 0 and 1 , respectively, in the measurement.

  (iii) How can the above circuit be used to determine (with high probability) whether the two states $|\psi\rangle$ and $|\phi\rangle$ are identical or not? [Assume that you are given arbitrarily many copies of the three input states and that the quantum circuit can be used arbitrarily many times.]

  comment

• Paper 3, Section II, C

  Quantum Information and Computation

  Part II, 2020

  Consider the quantum oracle $U_{f}$ for a function $f: B_{n} \rightarrow B_{n}$ which acts on the state $|x\rangle|y\rangle$ of $2 n$ qubits as follows:

  $$U_{f}|x\rangle|y\rangle=|x\rangle|y \oplus f(x)\rangle$$

  The function $f$ is promised to have the following property: there exists a $z \in B_{n}$ such that for any $x, y \in B_{n}$,

  $$[f(x)=f(y)] \text { if and only if } x \oplus y \in\left\{0^{n}, z\right\}$$

  where $0^{n} \equiv(0,0, \ldots, 0) \in B_{n}$.

  (a) What is the nature of the function $f$ for the case in which $z=0^{n}$, and for the case in which $z \neq 0^{n}$ ?

  (b) Suppose initially each of the $2 n$ qubits are in the state $|0\rangle$. They are then subject to the following operations:

  1. Each of the first $n$ qubits forming an input register are acted on by Hadamard gates;

  2. The $2 n$ qubits are then acted on by the quantum oracle $U_{f}$;

  3. Next, the qubits in the input register are individually acted on by Hadamard gates.

  (i) List the states of the $2 n$ qubits after each of the above operations; the expression for the final state should involve the $n$-bit "dot product" which is defined as follows:

  $$a \cdot b=\left(a_{1} b_{1}+a_{2} b_{2}+\ldots+a_{n} b_{n}\right) \bmod 2$$

  where $a, b \in B_{n}$ with $a=\left(a_{1}, \ldots, a_{n}\right)$ and $b=\left(b_{1}, \ldots, b_{n}\right)$.

  (ii) Justify that if $z=0^{n}$ then for any $y \in B_{n}$ and any $\varphi(x, y) \in\{-1$, $+1\}$, the following identity holds:

  $$\| \sum_{x \in B_{n}} \varphi(x, y)|f(x)\rangle\left\|^{2}=\right\| \sum_{x \in B_{n}} \varphi(x, y)|x\rangle \|^{2}$$

  (iii) For the case $z=0^{n}$, what is the probability that a measurement of the input register, relative to the computational basis of $\mathbb{C}^{n}$ results in a string $y \in B_{n}$ ?

  (iv) For the case $z \neq 0^{n}$, show that the probability that the above-mentioned measurement of the input register results in a string $y \in B_{n}$, is equal to the following:

  zero for all strings $y \in B_{n}$ satisfying $y \cdot z=1$, and $2^{-(n-1)}$ for any fixed string $y \in B_{n}$ satisfying $y \cdot z=0$.

  [State any identity you may employ. You may use $(x \oplus z) \cdot y=(x \cdot y) \oplus(z \cdot y), \forall x, y, z \in B_{n}$.]

  comment

• Paper 1, Section I, $10 D$

  Quantum Information and Computation

  Part II, 2021

  Alice wishes to communicate to Bob a 1-bit message $m=0$ or $m=1$ chosen by her with equal prior probabilities $1 / 2$. For $m=0$ (respectively $m=1$ ) she sends Bob the quantum state $\left|a_{0}\right\rangle$ (respectively $\left|a_{1}\right\rangle$ ). On receiving the state, Bob applies quantum operations to it, to try to determine Alice's message. The Helstrom-Holevo theorem asserts that the probability $P_{S}$ for Bob to correctly determine Alice's message is bounded by $P_{S} \leqslant \frac{1}{2}(1+\sin \theta)$, where $\theta=\cos ^{-1}\left|\left\langle a_{0} \mid a_{1}\right\rangle\right|$, and that this bound is achievable.

  (a) Suppose that $\left|a_{0}\right\rangle=|0\rangle$ and $\left|a_{1}\right\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)$, and that Bob measures the received state in the basis $\left\{\left|b_{0}\right\rangle,\left|b_{1}\right\rangle\right\}$, where $\left|b_{0}\right\rangle=\cos \beta|0\rangle+\sin \beta|1\rangle$ and $\left|b_{1}\right\rangle=$ $-\sin \beta|0\rangle+\cos \beta|1\rangle$, to produce his output 0 or 1 , respectively. Calculate the probability $P_{S}$ that Bob correctly determines Alice's message, and show that the maximum value of $P_{S}$ over choices of $\beta \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right]$ achieves the Helstrom-Holevo bound.

  (b) State the no-cloning theorem as it applies to unitary processes and a set of two non-orthogonal states $\left\{\left|c_{0}\right\rangle,\left|c_{1}\right\rangle\right\}$. Show that the Helstrom-Holevo theorem implies the validity of the no-cloning theorem in this situation.

  comment

• Paper 2, Section I, 10D

  Quantum Information and Computation

  Part II, 2021

  Let $\mathcal{B}_{n}$ denote the set of all $n$-bit strings and let $f: \mathcal{B}_{n} \rightarrow \mathcal{B}_{1}$ be a Boolean function which obeys either

  (I) $f(x)=0$ for all $x \in \mathcal{B}_{n}$, or

  (II) $f(x)=0$ for exactly half of all $x \in \mathcal{B}_{n}$.

  Suppose we are given the $n$-qubit state

  $$|\xi\rangle=\frac{1}{\sqrt{2^{n}}} \sum_{x \in \mathcal{B}_{n}}(-1)^{f(x)}|x\rangle$$

  Show how we may determine with certainty whether $f$ is of case (I) or case (II).

  Suppose now that Alice and Bob are separated in space. Alice possesses a quantum oracle for a Boolean function $f_{A}: \mathcal{B}_{n} \rightarrow \mathcal{B}_{1}$ and Bob similarly possess a quantum oracle for a Boolean function $f_{B}: \mathcal{B}_{n} \rightarrow \mathcal{B}_{1}$. These functions are arbitrary, except that either

  (1) $f_{A}(x)=f_{B}(x)$ for all $x \in \mathcal{B}_{n}$, or

  (2) $f_{A}(x)=f_{B}(x)$ for exactly half of all $x \in \mathcal{B}_{n}$.

  Alice and Bob each have available a supply of qubits in state $|0\rangle$ and each can apply local quantum operations (including their own function oracle) to any qubits in their possession. Additionally, they can send qubits to each other.

  Show how Bob may decide with certainty which case applies, after he has received $n$ qubits from Alice. [Hint: You may find it helpful to consider the function $h(x)=$ $f_{A}(x) \oplus f_{B}(x)$, where $\oplus$ denotes addition mod 2.]

  comment

• Paper 3 , Section I, D

  Quantum Information and Computation

  Part II, 2021

  Let $|\psi\rangle_{A B}$ be the joint state of a bipartite system $A B$ with subsystems $A$ and $B$ separated in space. Suppose that Alice and Bob have access only to subsystems $A$ and $B$ respectively, on which they can perform local quantum operations.

  Alice performs a unitary operation $U$ on $A$ and then a (generally incomplete) measurement on $A$, with projectors $\left\{\Pi_{a}\right\}$ labelled by her possible measurement outcomes $a$. Then Bob performs a complete measurement on $B$ relative to the orthonormal basis $\{|b\rangle\}$ labelled by his possible outcomes $b$.

  Show that the probability distribution of Bob's measurement outcomes is unaffected by whether or not Alice actually performs the local operations on $A$ described above.

  comment

• Paper 4, Section I, $10 D$

  Quantum Information and Computation

  Part II, 2021

  Let $\mathcal{H}$ be a state space of dimension $N$ with standard orthonormal basis $\{|k\rangle\}$ labelled by $k \in \mathbb{Z}_{N}$. Let QFT denote the quantum Fourier transform $\bmod N$ and let $S$ denote the operation defined by $S|k\rangle=|k+1 \bmod N\rangle$.

  (a) Introduce the basis $\left\{\left|\chi_{k}\right\rangle\right\}$ defined by $\left|\chi_{k}\right\rangle=\mathrm{QFT}^{-1}|k\rangle$. Show that each $\left|\chi_{k}\right\rangle$ is an eigenstate of $S$ and determine the corresponding eigenvalue.

  (b) By expressing a generic state $|v\rangle \in \mathcal{H}$ in the $\left\{\left|\chi_{k}\right\rangle\right\}$ basis, show that QFT $|v\rangle$ and QFT $(S|v\rangle)$ have the same output distribution if measured in the standard basis.

  (c) Let $A, r$ be positive integers with $A r=N$, and let $x_{0}$ be an integer with $0 \leqslant x_{0}<r$. Suppose that we are given the state

  $$|\xi\rangle=\frac{1}{\sqrt{A}} \sum_{j=0}^{A-1}\left|x_{0}+j r \bmod N\right\rangle$$

  where $x_{0}$ and $r$ are unknown to us. Using part (b) or otherwise, show that a standard basis measurement on QFT $|\xi\rangle$ has an output distribution that is independent of $x_{0}$.

  comment

• Paper 2, Section II, D

  Quantum Information and Computation

  Part II, 2021

  Alice and Bob are separated in space and can communicate only over a noiseless public classical channel, i.e. they can exchange bit string messages perfectly, but the messages can be read by anyone. An eavesdropper Eve constantly monitors the channel, but cannot alter any passing messages. Alice wishes to communicate an $m$-bit string message to Bob whilst keeping it secret from Eve.

  (a) Explain how Alice can do this by the one-time pad method, specifying clearly any additional resource that Alice and Bob need. Explain why in this method, Alice's message does, in fact, remain secure against eavesdropping.

  (b) Suppose now that Alice and Bob do not possess the additional resource needed in part (a) for the one-time pad, but that they instead possess $n$ pairs of qubits, where $n \gg 1$, with each pair being in the state

  $$|\psi\rangle_{A B}=t|00\rangle_{A B}+s|11\rangle_{A B},$$

  where the real parameters $(t, s)$ are known to Alice and Bob and obey $t>s>0$ and $t^{2}+s^{2}=1$. For each qubit pair in state $|\psi\rangle_{A B}$, Alice possesses qubit $A$ and Bob possesses qubit $B$. They each also have available a supply of ancilla qubits, each in state $|0\rangle$, and they can each perform local quantum operations on qubits in their possession.

  Show how Alice, using only local quantum operations, can convert each $|\psi\rangle_{A B}$ state into $\left|\phi^{+}\right\rangle_{A B}=\frac{1}{\sqrt{2}}\left(|00\rangle_{A B}+|11\rangle_{A B}\right)$ by a process that succeeds with non-zero probability. [Hint: It may be useful for Alice to start by adjoining an ancilla qubit $|0\rangle_{A^{\prime}}$ and work locally on her two qubits in $\left.|0\rangle_{A^{\prime}}|\psi\rangle_{A B \cdot}\right]$

  Hence, or otherwise, show how Alice can communicate a bit string of expected length $\left(2 s^{2}\right) n$ to Bob in a way that keeps it secure against eavesdropping by Eve.

  comment

• Paper 3, Section II, D

  Quantum Information and Computation

  Part II, 2021

  Let $\mathcal{B}_{n}$ denote the set of all $n$-bit strings and let $\mathcal{H}_{n}$ denote the space of $n$ qubits.

  (a) Suppose $f: \mathcal{B}_{2} \rightarrow \mathcal{B}_{1}$ has the property that $f\left(x_{0}\right)=1$ for a unique $x_{0} \in \mathcal{B}_{2}$ and suppose we have a quantum oracle $U_{f}$.

  (i) Let $\left|\psi_{0}\right\rangle=\frac{1}{2} \sum_{x \in \mathcal{B}_{2}}|x\rangle$ and introduce the operators

  $$I_{x_{0}}=I_{2}-2\left|x_{0}\right\rangle\left\langle x_{0}\right| \quad \text { and } \quad J=I_{2}-2\left|\psi_{0}\right\rangle\left\langle\psi_{0}\right|$$

  on $\mathcal{H}_{2}$, where $I_{2}$ is the identity operator. Give a geometrical description of the actions of $-J, I_{x_{0}}$ and $Q=-J I_{x_{0}}$ on the 2-dimensional subspace of $\mathcal{H}_{2}$ given by the real span of $\left|x_{0}\right\rangle$ and $\left|\psi_{0}\right\rangle$. [You may assume without proof that the product of two reflections in $\mathbb{R}^{2}$ is a rotation through twice the angle between the mirror lines.]

  (ii) Using the results of part (i), or otherwise, show how we may determine $x_{0}$ with certainty, starting with a supply of qubits each in state $|0\rangle$ and using $U_{f}$ only once, together with other quantum operations that are independent of $f$.

  (b) Suppose $\mathcal{H}_{n}=A \oplus A^{\perp}$, where $A$ is a fixed linear subspace with orthogonal complement $A^{\perp}$. Let $\Pi_{A}$ denote the projection operator onto $A$ and let $I_{A}=I-2 \Pi_{A}$, where $I$ is the identity operator on $\mathcal{H}_{n}$.

  (i) Show that any $|\xi\rangle \in \mathcal{H}_{n}$ can be written as $|\xi\rangle=\sin \theta|\alpha\rangle+\cos \theta|\beta\rangle$, where $\theta \in[0, \pi / 2]$, and $|\alpha\rangle \in A$ and $|\beta\rangle \in A^{\perp}$ are normalised.

  (ii) Let $I_{\xi}=I-2|\xi\rangle\langle\xi|$ and $Q=-I_{\xi} I_{A}$. Show that $Q|\alpha\rangle=-\sin 2 \theta|\beta\rangle+\cos 2 \theta|\alpha\rangle$.

  (iii) Now assume, in addition, that $Q|\beta\rangle=\cos 2 \theta|\beta\rangle+\sin 2 \theta|\alpha\rangle$ and that $|\xi\rangle=$ $U|0 \ldots 0\rangle$ for some unitary operation $U$. Suppose we can implement the operators $U, U^{\dagger}, I_{A}$ as well as the operation $I-2|0 \ldots 0\rangle\langle 0 \ldots 0|$. In the case $\theta=\pi / 10$, show how the $n$-qubit state $|\alpha\rangle$ may be made exactly from $|0 \ldots 0\rangle$ by a process that succeeds with certainty.

  comment